ACT, Inc. is the non-profit organization that administers the ACT college admissions test. They are the only source for official, previously released exams. Practice tests from third-party publishers like Kaplan or McGraw-Hill are just approximations. Fortunately ACT makes freely available previously administered tests. This post addresses the 60 questions in the Math section from the 2015-2016 ACT. This post and the answer explanations on Piqosity were contributed by undergraduate students at Rice University as part of a project for their class BUSI 390.
(Skip this guide and start working through the practice test with answer explanations)
Hello! If you’re here, you’re definitely on your way to becoming a better ACT Test-taker, as well as improving your standardized testing abilities in general. So keep powering through, and welcome, from Sarah Chou, Alex Young, and Michelle Lee!
ACT Math Test General Strategies
- Draw pictures when it gets confusing. Don’t be afraid to spend time organizing the picture of your thoughts, especially if it can prevent you from making silly mistakes and having to go back and figure out what’s wrong, which can take even more time.
- Plug in the answer choices to quickly check your work. With questions that ask you to solve variables, this is a quick way to make sure you didn’t make a silly mistake.
- Eliminate incorrect answer choices. You might not know the correct answer but chances are you can eliminate a few obviously wrong ones. Since you don’t get penalized for incorrect answers on the ACT (or the new SAT), eliminate as many choices as possible and make a guess!
- Skip difficult questions and come back later. All the questions are worth the same number of points. So why not maximize your wins and get all the easy ones (for you) down first? :)
Analysis of ACT Math Tested Concepts
Piqosity.com now features about 1700 adaptive test prep questions for the ACT or the equivalent of nearly 8 full-length practice tests. Of those 1700 questions, 903 are math questions. These questions break down into the following categories:
- Algebra and Coordinate Geometry – 448 questions
- Pre-Algebra and Elementary Algebra – 313 questions
- Plane Geometry and Trigonometry – 142 questions
Tips on Concepts in the 2015 ACT Math Practice Test
- Questions with variables
Questions with variables seem easy, but they’re also easy to make mistakes with. Plug in the answer you find with the question to check your work quickly. If you’re having trouble finding the answer, plug in answer choices to see which value makes both sides of the equation equal each other.
Given f = cd3, f = 450, and d = 10, what is c?
- 0.45
- 4.5
- 15
- 45
- 150
Answer: F. 0.45
- First we need to plug in 450 for f and 10 for d. The new equation is 450 = c(103)
- Since 103= 1,000 the equation can be rewritten as 450 = 1,000c.
- If we divide each side by 1,000, we get c = .45
While the solution can be found by isolating the variable that we are trying to find (c in this case), we can also solve the question by seeing which values in the answer choices work and which don’t. Since f = 450 and d3=1000, our new equation is 450 = c(1000). If we plug in the answer choices, we see that (0.45)(1000) = 450 and that (4.5)(1000) ≠ 450, (15)(1000) ≠ 450, (45)(1000) ≠ 450, and (150)(1000) ≠ 450. Plugging in the answer choices is a good way to check your answers or solve the problem if you’re having trouble with the Algebra.
- More questions with variables
When you cannot directly plug in the given answer choices into an equation with variables, plug in random numbers (and make note of which variables are which numbers) to find the answer. This is useful if doing the algebra is too complicated for you!
A formula to estimate the monthly payment, p dollars on a short-term loan is
where a dollars is the amount of the loan, r is the annual interest rate expressed as a decimal, and y years is the length of the loan. When a is multiplied by 2, what is the effect on p ?
- p is divided by 6
- p is divided by 2
- p does not change
- p is multiplied by 2
- p is multiplied by 4
Answer: D. p is multiplied by 2
Since everything else is held constant and a is in the numerator on the right side of the equation, if we double the value of a we should double the value of p.
When looking at this problem, it’s easy to get intimidated by all of the different variables that we don’t know the value of. However, since we’re only changing the value of one variable we can keep all of the others constant. An easy way to do this is to plug in random values of your choice for the variables. For instance, let’s say that a = 1, r = 2, and y = 3. Plugging this into the equation, we get p =((½)(1)(2)(3)+(1))/(12(3)) = 4/36 = 1/9. Now, let’s multiply a by 2 so that a = 2, and keep r = 2 and y = 3. Now, our equation is ((½)(2)(2)(3)+(2))/(12(3)) = 8/36 = 2/9, which is twice the value of our previous answer. You can plug in any values for the variables in this equation and get the same result.
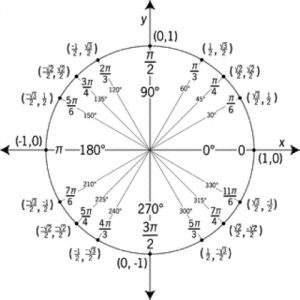
- The Unit Circle, aka Sine & Cosine Questions
The Unit Circle is an important trigonometry concept that can help you save time.
Being able to draw or visualize the important parts of the unit circle can also help you check and compare similar answers, such as the choices F, G, and H in the example question below.
The sides of an acute triangle measure 14 cm, 18 cm, and 20 cm, respectively. Which of the following equations, when solved for θ, gives the measure of the smallest angle of the triangle?
(Note: For any triangle with the sides of length a, b, and c that are opposite angles A, B, and C, respectively, (sin A)/a = (sin B)/b = (sin C)/c and c2 = a2 + b2 – 2ab cos C.)
- (sin θ)/14 = 1/18
- (sin θ)/14 = 1/20
- (sin θ)/20 = 1/14
- 142 = 182 + 202 – 2(18)(20)cos θ
- 202 = 142 + 182 – 2(14)(18)cos θ
Answer: J
To eliminate choices and save time, first compare F, G, and H. The answer choice F can be rewritten as sin θ= 14/18. This fraction is larger than G) sin θ= 14/20. The larger the fraction is, when sin θ<1, the larger the θ will be (think of a unit circle). Answer choice H is sin θ= 20/14 which is impossible because sin θ cannot be greater than 1. Therefore, eliminate H. Of the first three choices, G would be the smallest θ.
Now, look at J and K. Solve for θ using a calculator. Find that J is the smaller θ of the two, and then solve for sin θ= 14/20. These calculations prove that J gives the measure of the smallest angle of the triangle.
- Important Formulas & Calculator Efficiency
The Quadratic Equation
Other ways to solve this problem are to graph the equation p2 – 500p + 60,000 = 0 in a graphing calculator and find the x-intercept. In addition, some calculators have the ability to directly solve equations, including quadratic equations, and this can be much more efficient and less mistake-prone than solving by hand.
An artist makes a profit of (500p – p2) dollars from selling p paintings. What is the fewest number of paintings the artist can sell to make a profit of at least $60,000 ?
- 100
- 150
- 200
- 300
- 600
Answer: H. 200
- First, set 60,000 = (500p – p2)
- Then, rearrange the equation to a quadratic equation p2 – 500p + 60,000 = 0. Use the formula for quadratic equations (ax2 +/- bx + c) to find p.
- Plug in the numbers: a = 1, b = 500 (note: two negatives makes a positive) and c = 60,000
- Solving this out, x = 200 and x = 300. The fewest number of paintings is 200.
5. Long Questions
Some questions have a lot of words, pictures and numbers. Don’t be intimidated by these questions. Go to the question, which is normally at the end of the paragraphs, and get a general idea of what will be asked. Then pick out relevant information by underlining or circling what you really need to know.
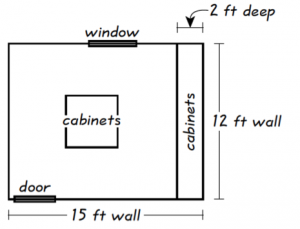
Gianna is converting 12-foot-by-15-foot room in her house to a craft room. Gianna will install tile herself but will have CC Installations build and install the cabinets. The scale drawing shown below displays the location of the cabinets in the craft room (0.25 inch represents 2 feet).
Cabinets will be installed along one of the 12-foot walls from floor to ceiling, and 4 cabinets that are each 3 feet tall will be installed in the middle of the room. These are the only cabinets that will be installed, and each of them will be 2 feet wide and 2 feet deep. CC Installations has given Gianna an estimate of $2,150.00 for building and installing the cabinets.
Gianna will install tile on the portion of the floor that will NOT be covered by cabinets. What is the area, in square feet, of the portion of the floor that will NOT be covered by cabinets?
- 72
- 90
- 140
- 156
- 164
Answer: H
One way to tackle the problem is to find the total area and then subtract the area of cabinets.
- To find the total area we calculate 12 ft x 15 ft = 180 square feet.
- The area of cabinets on the right wall are 12 ft long and 2 ft deep. Thus, we calculate 12 ft x 2 ft = 24 square feet.
- There are 4 cabinets in the room that are each 2 ft wide and 2 ft deep. (Note: We do not factor in the height of the cabinets in this problem). Doing the math we get: 4 x 2 ft x 2 ft = 16 square feet.
- Now that we know the total area and the area of the two cabinet sections, we calculate: 180 square ft – 24 square ft – 16 square ft = 140 square ft. This is the area of the floor that is not covered by cabinets and the correct answer.
This question throws a lot of information at you, but a lot of it isn’t relevant to this particular question. To find the area of the floor, we don’t need to know that the cabinets are 3 feet tall or that CC installations has a $2,150.00 estimate for the project, or that the room has a door and a window. With complicated questions like this, it’s important to read what the question is asking and find the information that will help you solve that particular question. One way to do this underline or jot a quick note of all of the information that helps you solve the problem. Extraneous information has the potential to distract you from the question and slow you down.
Good Luck!
When we were studying for the SAT and ACT in high school, we practiced with a lot of old exams to get ourselves prepared for the testing style and duration of the exam. We would study the questions we got wrong, and see why we missed them.
We’d take note of what kind of concept they tested (geometry, algebra) and made a notes sheet of important things we learned from these mistakes.
Take practice tests seriously, ideally at the time of the real exam, to train your body. We’re not morning people, but we had to take the ACT at 8 am, so we prepared ourselves by practicing early in the morning! Work hard, and you’ll do great!
Let’s Practice
Through the link below, you’ll find a practice quiz that contains all 60 of the questions from the previously released 2015-2016 ACT. If you want to simulate a more realistic testing environment, limit yourself to the test-allowed 60 minutes. After you take the test, you’ll get instant results, answer explanations, and detailed analysis of your performance.
These questions are the property of ACT, Inc., but the answer explanations were provided by the students who authored this blog post.
Take the Test or Download the PDF of the 2015-2016 ACT


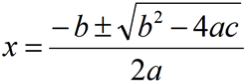


Leave A Comment