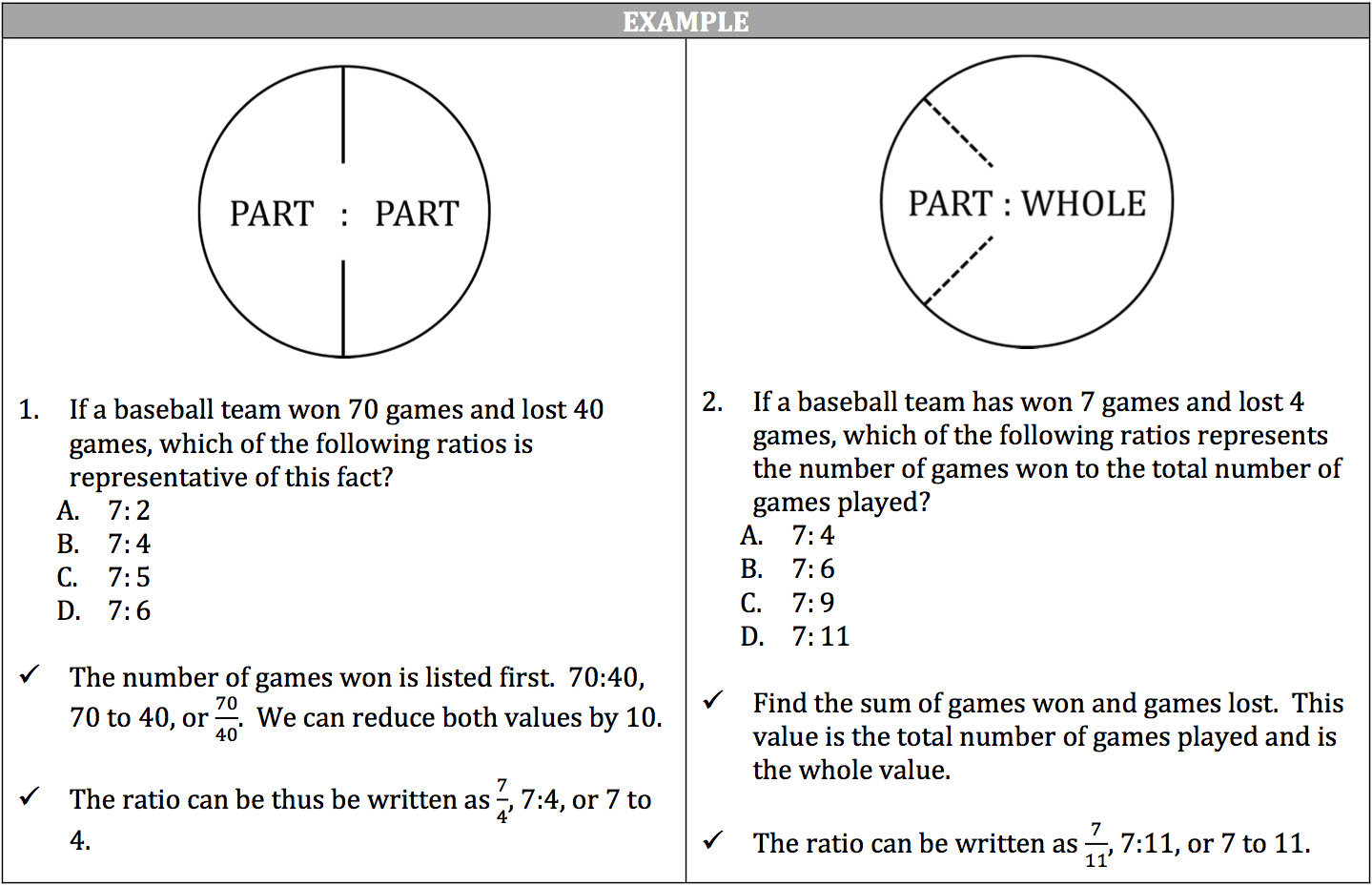
A ratio demonstrates a mathematical relationship between two quantities, and can be represented as a fraction, two numbers joined by a colon, or two numbers joined by the word “to.”
If the ratio is a fraction, generally the first value mentioned goes in the numerator while the second value goes in the denominator. If the ratio is in the other two forms, generally the first value mentioned is written first while the second value mentioned is written second.
A ratio can represent a relationship between values that are parts of a whole (part to part) or a relationship between a part and its whole (part to whole). Because the ratio can be represented as a fraction, you must reduce the ratio to its simplest form.
A proportion is two ratios set equal to one another. Proportions can help solve questions about scales of size or distance, such as a map or model. It is important that the placement of the known quantities in both ratios makes sense in proportions. For example, if a man stands 6 feet tall and has a 10 foot shadow, you can then determine the height of a nearby building with a 20 foot shadow through a proportion.

The ratios must be set up where the relationship between the values makes sense. The man’s height creates the length of his shadow, as does the building. Thus, the height of the man and the building can be placed in the numerator of each ratio, while their shadow lengths can be placed in the denominators of each ratio.

The proportion DOES NOT make sense if you place the height of the building over the man’s shadow length or the man’s height over the building shadow length.




Leave A Comment