You know that 2 is a larger number than 1, and you know that ‐2 is a smaller number than ‐1, so how do you show both of these statements to be true? While an equation is a demonstration of two quantities equal to one another, inequalities demonstrate two quantities not equal to one another. This includes algebraic expressions. You can show this relationship of inequality in four ways:

The nice thing about solving algebraic inequalities is that the process is the same as balancing algebraic equations and solving absolute value in algebraic equations. The only difference is that whenever you multiply or divide both sides of the inequality by a negative number the direction of the sign switches.

Showing or graphing inequalities on a number line isn’t very different from showing a value on a number line. The only difference is that an inequality will have many solutions.


Compound Inequalities
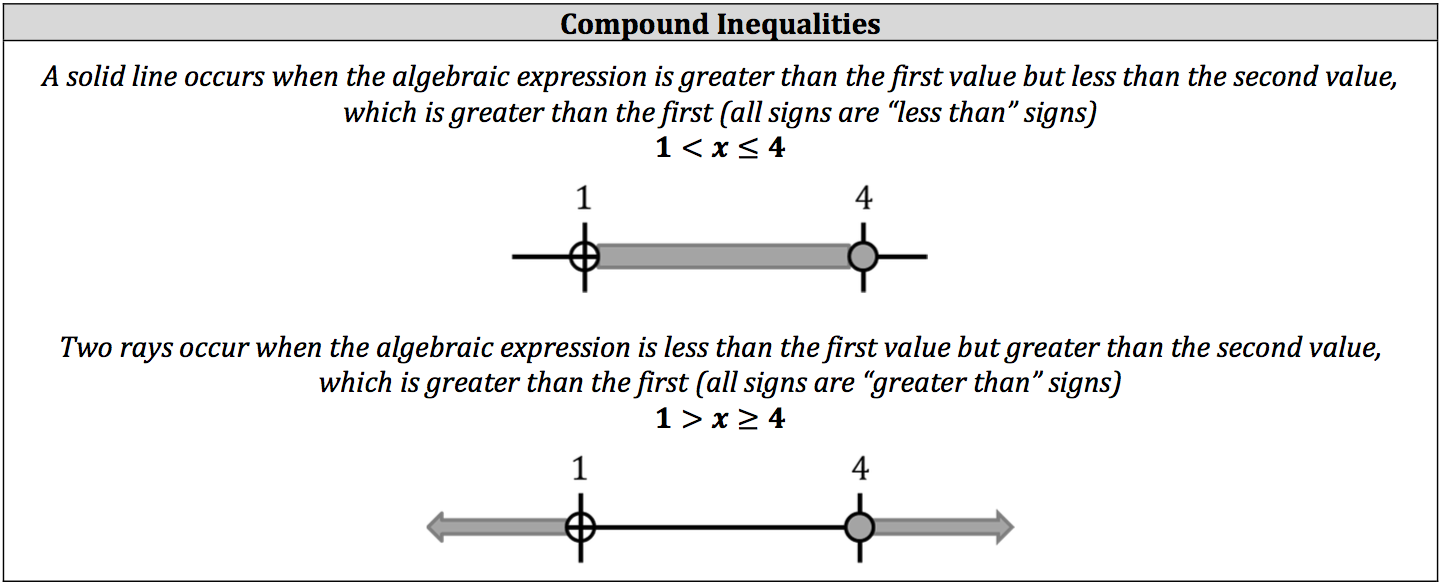
Sometimes, algebraic inequalities are compared to more than one value or an algebraic inequality has more than one set of solutions (absolute value of an inequality). These cases are called compound inequalities and can be represented in a series of inequality signs or two or more statements of inequalities joined by a conjunction. Compound inequalities are graphed in a similar manner to single inequalities, but will either have two rays or a solid line.




NICE STUFF CAUSE I HAVE A TEST RETAKE