Below are answer explanations to the full-length Math test of the previously released ACT from the current 2020-2021 “Preparing for the ACT Test” (form 1874FPRE) free study guide available here from ACT for free.
The ACT Math test explained below begins on page 24 of the guide. Please note that the 2020-2021 guide features the same practice test as the 2019-2020 guide. Other answer explanations in this series of articles:
- English Answer Explanations from 2020 ACT Practice Test
- Math Answer Explanations from 2020 ACT Practice Test (this article)
- Reading Answer Explanations from 2020 ACT Practice Test
- Science Answer Explanations from 2020 ACT Practice Test
- Writing Test Sample Essays from 2020 ACT Practice Test
When you’re finished reviewing this official practice ACT test, start practicing with our own 10 full-length practice ACT tests—absolutely free during the pandemic.
ACT Math Test Answer Explanations
Question 1, “Marcus’s favorite casserole.” The correct answer is “10.”
This question tests your understanding of ratios and proportions.
- First, find out how many servings each egg yields.
- We know that the original recipe calls for 3 eggs and makes 6 servings, meaning that each egg yields 2 servings (divide 6 servings by 3 eggs, which gives you 2 servings per egg).
- Marcus is increasing the number of eggs from 3 eggs to 5 eggs. Since we found that each egg yields two servings, simply multiply 5 eggs by 2 servings to get 10 total servings for the new recipe, which is the correct answer.
Note, you could have also noticed that Marcus was “not quite doubling” the recipe, which originally made 6 servings. As such, 12 servings would be too many (wrong answer), and 8 servings would be too little (wrong answer), which would have easily highlighted 10 as the correct answer.
Question 2, “History Club.” The correct answer is “1/32.”
This question tests your understanding of probability, which is represented as a fraction where the number of possibilities of a certain event occurring (numerator) is divided by the total number of outcomes (denominator).
- First, determine the total number of outcomes. We know that the History Club contains 35 members, but 3 of these are officers, who cannot be representatives for the club. Subtract 3 from 35 to find that there are only 32 possible people who can be representatives.
- Next, determine the total number of possibilities. Out of these 32 possible people, each person has the same chance of 1, since they are an individual, of being chosen randomly as the representative. Since Hiroko is not an officer of the club, we know that he is included as one of the 32 possibilities, meaning that the probability of him being chosen is 1/32, which is the correct answer.
Note, answer choices 0 can be eliminated right away because Hiroko is not an officer, meaning that his chances of being chosen as a representative are greater than 0. Answer choice ⅓ can also be eliminated immediately because Hiroko is not one of the 3 officers which is represented in the ⅓ answer choice.
Question 3, “22x+7 = 215.” The correct answer is “4.”
This question tests your understanding of solving algebraic equations. This question may seem daunting due to its exponential form, but it can be easily broken down. Exponents typically take the form of baseexponent.
- The base of each exponent is 2. Because they are the same, the base of each exponent on both sides of the equation can be ignored. Thus, the equation 22x+7 = 215 can be simplified to 2x + 7 = 15.
- Next, isolate 2x by subtracting 7 from each side in order to get 2x = 8.
- Finally, divide each side by 2 to get x = 4, which is the correct answer.
Question 4, “f(x) = 5x2 – 7(4x+3).” The correct answer is “-60.”
This question tests your understanding of function notation, which is simply a way to denote a function. It is representative of an equation y=f(x).
- First, plug in 3 in the place of x in the expression f(x) = 5x2 – 7(4x+3) to get f(3) = 5*(3)2 – 7(4*3 + 3).
- Next, expand the exponent in the first term to get 5×9 which is equal to 45.
- Next, apply PEMDAS (parentheses, exponents, multiplication, division, addition, subtraction) in order to expand 7(4*3 + 3). From this, we get 7(12 + 3) which is equal to 7(15), which can be multiplied out to get 105.
- Finally, subtract the second term from the first term to get 45 – 105 = -60, which is the correct answer.
Question 5, “Wallet reward.” The correct answer is “2/5.”
This question tests your understanding of probability, which is represented as a fraction where the number of possibilities of a certain event occurring (numerator) is divided by the total number of outcomes (denominator).
- First, determine the total number of outcomes by adding up the number of bills in the wallet. 5 + 7 + 8 = 20, meaning that there are 20 possible outcomes (numerator).
- Next, we know that there are 8 twenty-dollar bills, meaning that the probability of drawing a twenty dollar bill is 8 twenty-dollar bills divided by 20 total bills.
- This fraction 8/20 can be simplified by dividing both the numerator and the denominator by 4 to get ⅖, which is the correct answer.
Question 6, “ABC Book Club.” The correct answer is “5.”
This question tests your ability to solve word problems. First, express each book club’s charges in terms of an algebraic expression.
- We know that the ABC Book Club charges a $40 fee regardless of how many books you read in addition to charging $2 for every book you read. Set the number of books you read equal to x in order to get the expression: 2x + 40 = ABC Book Club’s charges.
- Do the same for the Easy Book Club, setting x equal to the number of books you read, in order to get the expression: 3x + 35 = Easy Book Club’s charges.
- In order to find out how many books must be read in order for the total charges from each club to be equal, set the two expressions equal to each other: 2x + 40 = 3x + 35.
- Then, solve the algebraic equation by combining like terms. This can be done by subtracting 2x from each side of the equation and then subtracting 35 from each side of the equation to get 5 = x. Thus, the number of books that must be read is 5, which is the correct answer.
Question 7, “Parallelogram.” The correct answer is “83°.”
This question tests your understanding of geometry. First, recognize that the diagonal AC separates the parallelogram into two congruent triangles.
- Second, recognize that opposite angles in a parallelogram are congruent, meaning that ∠ABC = ∠ADC = 40°.
- We now know two of three angles in the triangle CAD, since ∠ACD = 57° and ∠ADC = 40°. One of the properties of triangles is that the sum of interior angles of a triangle always equal 180°.
- Thus, since ∠ACD + ∠ADC + ∠CAD = 180°, we can solve for ∠CAD by plugging the values of the two known angles into the previous equation in order to get 57° + 40° + ∠CAD = 180°.
- This equation can be simplified into 97° + ∠CAD = 180°, and after subtracting 97 from each side, we find that ∠CAD = 83°, which is the correct answer.
Note, this question can also be solved by extending the line segment BA past point A so that all three angles can be represented on a straight line. This would form a new point, E, with a line segment extending from B to E.
Based on the properties of parallelograms, you know that ∠ABC = ∠DAE. ∠ADC and ∠BAC are interior angles that are congruent, thus ∠ADC = ∠BAC. You know that ∠DAE + ∠BAC + ∠CAD = 180° because they lie on a straight line.
From substitution, we get the same equation 57° + 40° + ∠CAD = 180°, which can be solved to find that ∠CAD = 83°.
Question 8, “.” The correct answer is “ 2.”
This question tests your understanding of algebraic expressions and fractions.
- First, plug in x = ½ into the expression
to get
, which can also be written as [8(½) – 3]/(½)
- Next, simplify the numerator by multiplying 8 by ½ to get 4, so that the numerator is now 4 – 3. Simplify this even further via subtraction, which gives you a numerator of 1.
- This gives you the expression 1/(½). Division of a fraction is equivalent to multiplying the numerator by the reciprocal of the denominator. In order to divide 1 by ½, multiple 1 by the reciprocal of ½, which is 2.
- This gives you the expression
, which is equal to 2 and is the correct answer.
Question 9, “Midpoint of line segment.” The correct answer is “(2, 2).”
This question tests your understanding of geometry. The equation to find the midpoint of a line segment (also known as the midpoint formula) is given by (xm, ym) = ([x1 + x2]/2 , [y1 + y2]/2).
- First, find the x-coordinate of the midpoint by adding the x-coordinates of the end points and dividing by 2. Thus, we find that 3 + 1 = 4, and 4÷2 = 2, so the x-coordinate of the midpoint is 2.
- Next, find the y-coordinate of the midpoint by adding the y-coordinates of the endpoints and dividing by 2. From here, we find that 8 + (-4) = 4, and 4÷2 = 2, so the y-coordinate of the midpoint is 2.
- Since we know the x- and the y- coordinate of the midpoint, we can put them together in standard (x,y) coordinate form to get the midpoint is (2,2), which is the correct answer.
Note, answer choices (-2, -12) and (-1, -6) can be easily eliminated because the x-coordinates of both endpoints are positive, meaning that the x-coordinate of the midpoint will also be positive.
This means that the midpoint is located in either Quadrant I or Quadrant IV of the (x,y) coordinate plane. Additionally, the y-coordinate of the first endpoint is both positive and larger (in numerical value) than the y-coordinate of the second endpoint, which is negative.
We can deduce from this that the y-coordinate of the midpoint will be positive, which corresponds to Quadrant 1 and Quadrant III of the (x,y) coordinate plane. Thus, we can eliminate answer choice (4, -12), leaving us with two possibilities for the correct answer: (11/2, 3/2) and (2,2).
Question 10, “Water depth (graph).” The correct answer is “6.”
This question tests your ability to interpret a graph. This graph plots the water depth (y-axis) of a pier over time (x-axis), which is shown to follow a wave pattern.
- First, recognize that the greatest water depth can be found at the crest (highest point or maxima) of the wave, which corresponds to a value of 12 feet at both 0-hours and 13-hours).
- Next, recognize that the least water depth can be found at the trough (lowest point or minima) of the wave, which corresponds to a value of 6 feet at both 6-hours and 18-hours)
- You can find the positive difference between the greatest water depth and the least water depth by subtracting the least water depth of 6 feet from the greatest water depth of 12 feet to get 6, which is the correct answer.
Question 11, “Slope of the line through (-2,1).” The correct answer is “-3/2.”
This question tests your understanding of geometry. The equation to find the slope of a line is given by slope = rise/run = (y2 – y1)/(x2 – x1).
- We are given two points: (-2,1), which can be designated as (x1, y1) and (2,-5), which can be designated as (x2, y2).
- First, find the numerator of the slope by subtracting y1 from y2, which looks like this: -5 – 1 = -6.
- Next, find the denominator of the slope by subtracting x1 from x2, which looks like this: 2 – (-2) = 2 + 2 = 4.
- Finally, put this fraction together to get -6/4, which can be simplified by dividing both the numerator and denominator by 2. (-6÷2)/(4÷2) = -3/2 which is the correct answer.
Question 12, “Cherokee County.” The correct answer is “43.”
This question tests your ability to solve word problems.
- First, figure out the number of miles per hour by which Kirk exceeded the speed limit. We know that he was fined $221, and the fine for speeding is $17 for each mile per hour that you drive above the speed limit.
- We can divide the amount of Kirk’s fine, $221, by the rate of the fine, $17/mph to get 13 miles per hour. Here, the $ units cancel, and dividing by (1/mph) gives us the reciprocal: miles per hour.
- Now, since we know that Kirk exceeded the speed limit by 13 miles per hour, we can add this amount to the speed limit of 30 miles per hour to find Kirk’s total speed when he was fined. 30 mph + 13 mph = 43 mph, which is the correct answer.
Question 13, “Sum of the solutions.” The correct answer is “.”
This question tests your understanding of algebraic equations and fractions.
- In order to find the sum of the solutions of both equations, you must solve each equation individually.
- First, solve 8x = 12 by dividing each side by 8 to isolate the variable x; 8x/8 = 12/8 can be simplified into x = 12/8.
- This fraction can be further simplified by dividing both the numerator and denominator by their GCD (greatest common divisor), which is the largest positive integer that divides both 8 and 12. Both 12 and 8 can be divided by 4, their GCD, to get a simplified fraction of x = 3/2.
- Next, you must solve the second equation 2y + 10 = 22. In order to isolate y, subtract 10 from each side to get 2y = 12. Then, divide each side by 2 in order to solve for y, and you end up with y = 6.
- To find the sum of the solutions, add the value of x and the value of y together. 3/2 can also be expressed as 1.5, which makes it easier to add to 6. Thus, we find that 6 + 1.5 = 7.5, which can also be expressed as
, and this is the correct answer.
Question 14, “Average of 5 distinct scores.” The correct answer is “336.”
This question tests your understanding of averages. The average of a list of values is equal to the total sum of these values (numerator) divided by the number of items in the list (denominator). The median of a list is the middle number in a sorted (ordered based on numerical value) sequence.
- We are told that the sum of the 5 scores is 420, and that the average of these scores is the same as their median. From this, we can determine the value of the average, and correspondingly, the value of the median.
- An average can be calculated by adding up all of the data points and dividing by the number of data points. In this question, we don’t need to individually add up each data point because we have already been given the sum of the 5 data points: 420. Thus, the average is equivalent to 420/5, which can be simplified into 84.
- We know that this average value of 84 is the same as the value of the median. In order to find the sum of the 4 scores that are not the median, we must subtract the value of the median, 84, from the sum of the 5 scores, 420. 420 – 84 = 336, which is the correct answer.
Question 15, “| |-8+4| – |3 – 9| |.” The correct answer is “2.”
This question tests your understanding of absolute value, which is equivalent to a number’s distance from zero. This means that absolute value always results in a positive or zero value.
- First, isolate the two absolute value expressions and find their values. The two expressions are |-8 + 4| and |3 – 9|.
- To find the value of |-8 + 4|, simplify the expression inside of the absolute value brackets by adding -8 and 4 to get |-4|.
- |-4| is equal to 4, because absolute value turns negative values into positive values. You can also think of |-4| as the distance of -4 from 0, which is 4 units.
- The value of |3 – 9| can be found by subtracting 9 from 3 to obtain |-6|, which can be simplified into 6 because of the absolute value brackets.
- We still have to solve one more expression. The simplification of |-8 + 4| and |3 – 9| within | |-8 + 4| – |3 – 9| | results in the expression | 4 – 6 |.
- The value of this expression can be found by subtracting 6 from 4 to get |-2|, which is equal to 2, the correct answer.
Note: upon seeing the absolute value brackets that encapsulate the entire expression, the negative answer choices of -18 and -2 can be immediately eliminated because we know that finding absolute value will result in a positive or zero value.
Question 16, “x2/3.” The correct answer is “.”
This question tests your understanding of fractional exponents, which is a notation to express powers and roots together.
- First, we can rewrite x2/3 as
in order to separate the expression.
- One of the rules of exponents is that
= . This means that
.
- Another rule of radicals and exponents is that
. We can use this rule to rewrite
as
.
-
is the same as
, which is the correct answer.
Question 17, “Slope of 4x = 7y + 5.” The correct answer is “4/7.”
This question tests your understanding of geometry and equations of lines. The equation of any straight line can be written as y = mx + b, where m is the slope of the line and b is the y-intercept.
- We can rearrange the given equation 4x = 7y + 5 so that it matches the form y = mx + b. We do this by solving for y.
- First, we subtract 5 from each side to get 4x – 5 = 7y. Next, we divide each side by 7 to get
.
- This equation
matches the form y = mx + b. From here, we can see that the value of m is equal to
, which is the correct answer.
Note: you can skip one of the intermediate steps here. Since we know that we simply want to find m, which is the coefficient of x, we can divide each side by 7 to find the slope without subtracting 5 from each side first.
Question 18, “Integers m and n.” The correct answer is “m is an odd integer and n is an even integer.”
This question tests your understanding of numbers and operations.
- This question can be solved by a process of elimination and by substituting possible values for m and n to see whether their sum is even or odd.
- For the first answer choice, “m is an odd integer,” we can see what happens when n is an even integer and when n is an odd integer. Let’s suppose we set the value of m to 3. The integer n can either be even (suppose a value of 2) or odd (suppose a value of 3).
- The sum of odd integer m and even integer n gives 3 + 2, which equals 5, an odd integer. However, the sum of odd integer m and odd integer n gives 3 + 3, which equals 6, an even integer.
- Thus, answer choices “m is an odd integer” and “n is an odd integer” can be eliminated because neither of these choices will always yield an odd integer.
- Looking at the last three answer choices, we can eliminate “m and n are both odd integers” because we have already shown that the sum of odd integer m and odd integer n gives an even integer.
- For the next answer choice, “m and n are both even integers,” let us suppose that m = 2 and n = 4. The sum of 2 + 4 is 6, which is an even integer. Thus, this answer choice can be eliminated because the sum of two even integers will never yield an odd integer.
- Thus, we are left with the answer choice “m is an odd integer and n is an even integer,” which is the correct answer.
Note: after testing the first answer choice by substituting in real values for m and n, we know that the sum of odd integer m and even integer n gave 3 + 2 = 5, which is an odd integer. Utilizing this knowledge, we could have skipped the process of elimination of the other 4 answer choices, instead arriving immediately at the conclusion that the sum of odd integer m and even integer n will always give an odd integer.
Question 19, “Right Triangle ABC.” The correct answer is “20.”
This question tests your understanding of geometry.
- In order to find the distance from point A to the midpoint of AB, we must find the length of AB, which is also the hypotenuse of this right triangle. The hypotenuse can be found using the pythagorean theorem:
where c is the longest side of the triangle, aka the hypotenuse.
- We can set the given lengths of the 2 legs of the triangle equal to a and b, so that 32 = a and 24 = b.
- Next, we can find the hypotenuse of the triangle ABC by plugging these values into the equation
and solving for c.
- Plugging in the values gives
which can be simplified into
.
- This can be further simplified into
, and we can solve for c by taking the square root of each side. The square root of 1600 is 40, so c = hypotenuse = length of AB = 40.
- To find the distance between point A and the midpoint of AB, we simply divide the length of AB, 40, by 2 to get 20, which is the correct answer.
Question 20, “In ΔDEF.” The correct answer is “Cannot be determined from the given information.”
This question tests your understanding of geometry and trigonometry.
- We know that the pythagorean theorem only applies to right triangles. The question does not specify whether ΔDEF is a right triangle, therefore we cannot use the pythagorean theorem to determine the third side of this triangle.
- In order to find the third side of a non-right triangle, we could use the law of cosines:
, where D is the angle at point D and e, f, and d are the lengths of the triangle sides opposite to their corresponding angles of E, F, and D.
- However, we are not given any of the angles in this triangle. Therefore, we cannot use the law of cosines, and we are unable to determine the length of DF from the given information.
Question 21, “Laura plans to paint.” The correct answer is “340.”
This question tests your ability to solve word problems.
- Laura’s room is the shape of a rectangular prism, whose surface area can be calculated using the equation SA = 2(wl + hl + hw), where h = height, w = width, and l = length.
- We know that Laura only plans on painting the side walls of her room, not her ceiling or her floor. We can find the area of these walls by removing the “wl” portion of the surface area equation above, since the width×length of the room represents the area of the ceiling.
- Thus, the area of the walls in Laura’s room is A = 2(hl + hw). Plugging in the values for length, width and height gives A = 2[(8×10) + (8×15)].
- This can be simplified into A = 2[(80) + (120)], which can be further simplified into A = 2×200.
- We know that the area of Laura’s walls is equal to 2×200, or 400 square feet. However, we must subtract the area of her window and door, 60 square feet, from the area of her walls in order to find the area that she plans to paint.
- Thus, the area that Laura plans to paint is 340 square feet (400 – 60 = 340).
Note: this question can be more easily understood by drawing a rectangular prism to see which walls Laura plans to paint.
Question 22, “Width of the rectangle” The correct answer is “7.5.”
This question tests your understanding of geometry.
- The perimeter of a rectangle is equivalent to
where l = length and w = width. The length of this rectangle is 5 inches longer than the width. This can be represented by the expression
.
- We can find the width of the rectangle by plugging in the expression for l, which gives
, and solving for w.
- We know that the perimeter of the rectangle is 40 inches, and plugging in this value gives
.
- In order to solve this equation, divide each side by 2 to get
. Then, subtract 5 from each side to get
. Finally, by dividing each side by 2 in order to solve for w, you should get
, which is the correct answer.
Question 23, “8% of 60.” The correct answer is “24.”
This question tests your understanding of fractions and percentages.
- This question can be interpreted as an algebraic equation:
, where
= an unknown value.
- 8% can be simplified to
or 0.08, which gives
.
- We can solve this equation by multiplying each side by 5, which gives
, which can be simplified into
.
- Multiplying out these numbers gives
, which is the correct answer.
Question 24, “Armin’s season pass.” The correct answer is “13.”
This question tests your ability to solve word problems and inequalities.
- The cost of a season pass is $175, which the cost of a ticket is $14. We can solve this problem by setting up an inequality.
- If Armin wants to save money with the season pass, then the cost of the season pass ($175) must be less than the cost of going to games for the individual ticket price of $14. This can be represented by
.
- Divide each side of the inequality by 14 to get
. This means that Armin must go to at least 12.5 games to offset the price of the season pass. However, since he cannot go to “half” of a game, he must attend at least 13 games in order for the cost of his season pass to be less than the cost of buying individual tickets.
Question 25, “(4.8×10-7)/(1.6×10-11).” The correct answer is “3.0×104.”
This question tests your understanding of exponents.
can be solved by simplifying the coefficients and the exponents separately. Thus, we can rewrite
as
- 4.8 divided by 1.6 is the same as 48 divided by 16, which is 3. This gives us the expression
.
- The quotient rule of exponents states that
. We can apply this rule to get
. This can be simplified to
which is equal to
.
- Thus, we have found that
=
=
, which is the correct answer.
Question 26, “A circle has center C(-1,2).” The correct answer is “(-4,-2).”
This question tests your understanding of geometry.
- If line segment AB is a diameter of the circle, then it must pass through the center C. From this, we know that the distance between C and A is the same as the distance between C and B.
- We can begin to solve this problem by finding the slope of the line between point C(-1,2) and point A(2,6). Slope = rise/run = (y2 – y1)/(x2 – x1) =
. This can be simplified into slope =
.
- The slope of the line between C and B is the same as the slope of the line between C and A. Thus, we know that the value of the rise over run from point B to point C is 4/3.
- We can find the y-coordinate of point B by subtracting the “rise” or “y” value of the slope from the y-coordinate of C, and we can find the x-coordinate of point B by subtracting the “run” or “x” value of the slope from the x-coordinate of C. This is represented as (-1-3, 2-4) which can be simplified into (-4,-2), which is the correct answer.
Question 27, “a factor of x3 – 64.” The correct answer is “(x-4).”
This question tests your understanding of factoring.
- Both terms in
are perfect cubes, so this expression can be interpreted as the difference of two cubes. The factoring of a difference of cubes is given by the formula
.
- 64 is the equivalent of 43. From this, we can figure out that
.
- This can be simplified to
. The only answer choice that fits either of these terms is
, which is the correct answer.
Question 28, “The average of a list.” The correct answer is “94.”
This question tests your understanding of averages. The average of a list of values is equal to the total sum of these values (numerator) divided by the number of items in the list (denominator).
- Because the first 3 numbers are the same in each list, we can combine the values of each of these numbers and represent them as x.
- The average of the first list can be written as
. The average of the new list can be written as
where a = the new average. In order to find the new average, we must first solve for x so that we can plug it into our equation for the new average.
- In order to solve for x, we must multiply both sides of the first equation by 4 to get
. After subtracting 80 from 360, we find that
- We can solve for the new average by plugging this value into the equation
, which gives
. This can be further simplified into
. This gives us a final value of
, which is the correct answer.
Question 29, “Number line.” The correct answer is “![]() .”
.”
This question tests your understanding of number lines and physical representations of numbers.
- The value of a is -2.5, as indicated by its location at -2.5 on the number line. The location of
can be determined by finding the value of
.
- This can be simplified to give
. Thus, the correct answer choice is the one where
corresponds to 6.25 on the number line.
Question 30, “Maria’s pizza.” The correct answer is “.”
This question tests your understanding of fractions.
- If Maria only ate
of the pizza and gave the rest to her brothers, then her 3 brothers were given
of a pizza.
- To determine the fraction of the whole pizza that each brother will receive when split equally, we must divide
into 3 parts.
divided by 3 is equivalent to
.
- When multiplying fractions, you multiply the numerators together and the denominators together. This gives us
, which is the correct answer.
Question 31, “The number 1,001.” The correct answer is “.”
This question tests your understanding of prime numbers, which is a number that is not a product of two smaller numbers.
- To find the prime factorization of 30,030, first divide 30,030 by 1,001 to get 30. This means that
.
- Since we know that the prime factorization of 1,001 is
, we can plug this in for the prime factorization of 30,030. This gives us
.
- However, we can’t stop here because 30 is not a prime number, as it is the product of
,
, and
. To find the prime factorization of 30, first divide 30 by 2, the smallest prime number that is also a factor of 30.
- 30÷2 = 15, but this number can be further simplified by dividing by 3, the smallest prime number that is also a factor of 15. Thus, we find that 15÷3 = 5.
- From here, we know that the prime factors of 30 are
. We can plug these values into the prime factorization of 30,030.
- This gives us
, which is the correct answer.
Question 32, “Area of the park.” The correct answer is “544.”
This question tests your understanding of geometry and polygons.
- The park is in the shape of a trapezoid. The area of the trapezoid is given by the formula
, where a = one of the trapezoid bases and b = the other trapezoid base.
- The bases of a trapezoid are the two uneven, parallel sides of the trapezoid, while the height of a trapezoid is the distance between the two bases. From this, we can figure out that a = 28, b = 40, and h = 16 as represented in the diagram.
- We can find the area of the drawing of the park by plugging these values into the equation for the area of a trapezoid. Thus, we get
, which can be simplified into
.
- This can be further simplified into
, which gives us
Thus, the area of the drawing of the park is 544 square inches, which is the correct answer.
Question 33, “Perimeter of the park.” The correct answer is “156.”
This question tests your understanding of geometry and polygons.
- The park is in the shape of a trapezoid. To find the perimeter of the park, we must find the perimeter of the scale drawing and multiply it by the conversion rate of 1 inch = 1.5 feet.
- To find the perimeter of the scale drawing, we must find the length of the unknown leg. We can divide the drawing of the park into a right triangle and a rectangle with an imaginary line that is parallel to its altitude (which is also the height of 16 inches).
- The hypotenuse of this right triangle is the length of the unknown leg. We know that the length of one of the triangle’s legs is 16 inches. The length of the other leg is given by 40 inches minus 28 inches, which gives us 12 inches.
- We can use the Pythagorean theorem (
) to find the hypotenuse, c, of the triangle. It is easier to simplify the legs of the two triangles by dividing each value by 4, which gives us that the two triangle legs are 4 inches and 3 inches.
- Plugging these values into the Pythagorean formula, we get
. This can be simplified into
.
- Adding these values together gives us
, and taking the square root of each side gives us that
.
- However, this is not the actual hypotenuse of the right triangle. We must multiply
by 4 because we had previously scaled down the triangle to make the math easier.
- After scaling the hypotenuse back up, we find that
inches. To find the perimeter of the drawing of the park, we simply have to add 20 inches to the lengths of the other sides of the drawing.
- The perimeter of the scale drawing is given by 20 inches + 28 inches + 40 inches + 16 inches, which adds up to 104 inches.
- However, the question is asking for the perimeter, in feet, of the actual park, not the scale drawing of the park. We must multiply the perimeter of the scale drawing, 104 inches, by the conversion factor
to get the perimeter of the park in feet.
- Multiplying 104 by 1.5 results in a park perimeter value of 156 feet, which is the correct answer.
Question 34, “Length of the south side.” The correct answer is “.”
This question tests your understanding of fractions and percentages.
- Although the question asks about the lengths of the park, we know we can use the lengths of the scale drawing to answer this question because they are both scaled by the same factor.
- The length of the south side of the park is 40 inches. The length of the north side of the park is 28 inches. We can set up an equation to find the fraction of the length of the north side that is equivalent to the length of the south side.
- In words, this equation will look like “the length of the south side” = x × “the length of the north side.” To find the percentage that the question is asking for, we will have to multiply x by 100 in order to convert the fraction into a percentage.
- Plugging in the values of the length of the sides, we get the equation
.
- This can be simplified by dividing each side by 28 to get
. We can further simplify this fraction by dividing both the numerator and the denominator by 4, their greatest common factor, to get
.
- Multiplying by 100 to get the percentage gives us
. After plugging this into a calculator or solving by long division, we find that
, which is equivalent to
.
- We know that the correct answer is
, either by converting 142.86 back into partial fraction form or realizing that the only answer choice that is close to 142.86 is
.
Question 35, “Mr. Smith’s walkway.” The correct answer is “360.”
This question tests your understanding of geometry and area.
- The area of the walkway can be found by subtracting the area of the cabin from the area of the total floor plan. We know that the dimensions of the cabin are 24 feet by 30 feet, so the area of the cabin is equal to 24 × 30 = 720 square feet.
- The dimensions of the total floor plan are 36 feet by 30 feet, so the area of the total floor plan is 36 × 30= 1,080 square feet.
- By subtracting the area of the cabin, 720 square feet, from the area of the total floor plan, 1,080 square feet, we can find the area of the walkway around the cabin. This gives us 1080 – 720 = 360. The area of this walkway is 360 square feet, which is the correct answer.
Question 36, “Mrs. Smith curtains.” The correct answer is “354.”
This question tests your ability to solve word problems.
- We know that the cabin contains 3 small windows and 1 large window as indicated in the floor plan. We also know that the cabin has 3 rooms.
- Since this question asks for the value that is closest to the total price that Mrs. Smith will pay, we can round the value of the small window curtains from $39.50 to $40, since this is easier to multiply.
- To find the price of the small window curtains, we can multiply the price of each curtain, $40, by the number of small windows, 3. This gives us 40×3 = $120.
- The cost of the large window curtain is twice that of the small window curtain, which can be represented by 40×2. Thus, we know that Mrs. Smith has to pay $80 for the large window curtain.
- The cost of a ceiling fan is $52, and there are 3 rooms that Mrs. Smith is installing ceiling fans in. Thus, the cost of all three ceiling fans equals 523, which is equal to $156. (Note: you can also round $52 down to $50 and estimate the cost of the ceiling fans to be ∼$150).
- Finally, to find the total price that Mrs. Smith must pay, we simply have to add up the price of the small curtain windows, the price of the large curtain window, and the price of the three ceiling fans.
- So, the total price ≅ $120 + $80 + $156. This can be simplified into total price $356. The answer choice that is the closest to this value is $354, which is the correct answer.
Question 37, “Cabin roof.” The correct answer is “0.04.”
This question tests your understanding of probability, which is represented as a fraction where the number of possibilities of a certain event occurring (numerator) is divided by the total number of outcomes (denominator).
- If the chance of rain is independent of the day, then we can find the probability of it raining both days by multiplying the probability of it raining the first day by the probability of it raining the second day.
- The chance of rain on each day is 20%, or 0.20. The probability of it raining both days is given by P = (0.20)(0.20).
- Multiplying this out gives us P = 0.04, which is the correct answer.
Question 38, “An irrational number.” The correct answer is “.”
This question tests your understanding of exponents and irrational numbers, which are real numbers that cannot be written as fractions.
- This question must be solved by going through each answer choice and eliminating the incorrect ones.
- The first answer choice,
, can be rewritten as
based on the distributive rule of square roots.
can be further simplified into
. Using the same distributive rule, we can rewrite
as
, which equals
. Since
can be written as a fraction and it is a real number, this answer choice cannot be classified as an irrational number.
- The second answer choice,
, can be rewritten as
based on the distributive rule of square roots.
can be further simplified into
, which equals 2. Since 2 can be written as a fraction (
) and it is a real number, this answer choice cannot be classified as an irrational number.
- In the third answer choice,
, the square exponent is negating the square root around the 8. Thus,
can be simplified into 8. Since 8 can be written as a fraction (
) and it is a real number, this answer choice is not an irrational number.
- The fourth answer choice,
, can be rewritten as
based on the distributive rule of square roots.
can be further simplified into
, which equals 4. Since 4 can be written as a fraction (
) and it is a real number, this answer choice cannot be classified as an irrational number.
- We are left with one answer choice which must be correct because all of the other answer choices have been eliminated. However, we can check this by trying to simplify
.
can be simplified into
, which is equivalent to
. Thus we can simplify
into
. However,
cannot be simplified any further, and since it cannot be written as a fraction or a ratio, this answer choice is equivalent to an irrational number.
Question 39, “Value of tanθ.” The correct answer is “.”
This question tests your understanding of trigonometry.
- We can visualize this problem as a triangle by imagining a line segment perpendicular to the x-axis that runs through the point (10,4).
- Since θ is an acute angle in the triangle, we know that the tangent of θ is the ratio of the opposite side to the adjacent side.
- From the point (10,4) that we are given, we know that the length of the adjacent side is 10 units and the length of the opposite side is 4 units.
- Thus, the tangent of θ equals the ratio of 4 to 10. This can also be written as
, which can be simplified into
.
Question 40, “Equation |2x-8| + 3 = 5.” The correct answer is “2x – 8 = 2 and -(2x – 8)= 2.”
This question tests your understanding of algebraic equations and absolute notation, which is equivalent to a number’s distance from zero. Absolute notation always results in a positive or zero value.
- First, we must isolate the absolute notation on one side of the equation by subtracting 3 from each side. This gives us
.
- In order to find the pair of equations that gives the solutions to the initial equation, we can split the absolute value equation into two separate equations. The rule for absolute value states that
can be broken down into
and
.
- Thus, we can split
into
and
. The latter equation can be rewritten by multiplying each side by -1 to get
.
- The two equations whose solutions are equal to the solutions of
are
and
.
Question 41, “Ms. Hernandez’s science students.” The correct answer is “1.”
This question tests your ability to solve word problems and to interpret a frequency chart, which denotes the number of times a certain event or data value occurs.
- The frequency chart gives many overlapping score ranges. The first score range is 65-70, and the second score range is 65-80. We can deduce that subtracting the range of 65-70 from the range of 65-80 leaves the range of 71-80.
- To find the number of students who got a test score in the interval of 71-80, we can subtract the number of students in the 65-70 range (12 students) from the number of students in the 65-80 range (13 students).
- Thus, the number of students with a test score in the interval 71-80 is equal to 13 students minus 12 students. This equals 1 student, which is the correct answer.
Question 42, “Number of decibels.” The correct answer is “30.”
This question tests your understanding of logarithms. The basic rule of logarithms is that if , then
.
- First, plug in the sound intensity value into the equation
to find the number of decibels that are produced. This gives us
, where K is a constant that can be ignored.
- The equation can be simplified by condensing 1000 into the form of
, which gives us
.
- We know that the
, so
must equal 3. When we plug this back into the equation for d, we find that
. This simplifies into 30 decibels, which is the correct answer.
Question 43, “Mario plays basketball.” The correct answer is “213.”
This question tests your ability to solve word problems and to interpret a data table.
- In order to find the number of points that Mario scored, we have to calculate how many shots he completed for each type of shot. After that, we have to multiply his number of completions by how many points the type of shot was worth. This can be represented by Px = (# attempted)(fraction successful)(x points).
- Then, we have to add the points for each type of shot together.
- For 1-point free throws, we know that Mario made 75%, or
, of 80 shots. This can be represented by P1 =
, which equals 60 points.
- For 2-point field goals, we know that Mario made 90%, or
, of 60 shots. This can be represented by P2 =
, which can be simplified into P2 =
. This can be further simplified into P2 =
, which equals 108 points.
- For 3-point field goals, we know that Mario made 25%, or
, of 60 shots. This can be represented by P3 =
, which can be simplified into P3 =
. This equals 45 points.
- Finally, we can add up the points that Mario scored for each type of shot to get
. This adds up to 213 points, which is the correct answer.
Question 44, “Graph of y=|x – 6|.” The correct answer is “Translation to the right 6 coordinate units.”
This question tests your understanding of absolute value graphs and transformations.
- The general form of an absolute value equation is
, where a tells us how much the graph is stretched vertically, h tells us how far the graph shifts horizontally, and v tells us how far the graph shifts vertically.
- The equation
matches this form, where
. A positive value for h indicates that the graph is shifted to the right, while a negative value for h indicates that the graph is shifted to the left.
- Thus, a value of
indicates that the graph will be shifted, or translated, 6 units to the right.
Question 45, “Toby’s toy soldier.” The correct answer is “125.”
This question tests your understanding of word problems and geometry.
- In order to find the volume of the toy soldier, we can subtract the volume of the water in the rectangular container from the volume of the water with the toy submerged in it.
- The volume of the water in the rectangular container without the toy in it is given by
, where h is the height of the water, l is the length of the container, and w is the width of the container.
- Plugging in the values for these variables, we find that
, which can be simplified into
cubic centimeters.
- To find the volume of water with the submerged toy in it, we simply have to plug in the new height of the water into the equation for volume. Thus, we get
, which can be simplified into
.
- The volume of the toy soldier can be found by subtracting 192 from 316.8 (which can be rounded to 317 because the question is only asking for the closest answer). Thus, the volume of the toy soldier is about 125 cubic centimeters.
Question 46, “Box filled with packing material.” The correct answer is “.”
This question tests your ability to solve word problems and your understanding of geometry.
- The volume of the packing material in the box is equal to the volume of the cylinder subtracted from the volume of the box.
- The volume of the box is given by
, and plugging in the values from the question gives us
.
- The volume of a cylinder is given by the equation
. Plugging the values from the question in, we get
.
- Thus, the volume of the packing material is given by the expression “
.”
Question 47, “Room with a rectangular floor.” The correct answer is “35.”
This question tests your understanding of geometry and unit conversions.
- This question gives us the dimensions of the floor in feet but asks for the area of the floor in square yards. To find the square yardage of the floor, we must first convert the dimensions of the floor from feet into yards.
- There are 3 feet in a yard. Thus, the dimensions of the rectangular floor can be converted from 15 feet by 21 feet into 5 yards by 7 yards.
- The area of the floor in square yards is A = 5 yards × 7 yards. This equals 35 square yards, which is the correct answer.
Question 48, “ABC Cabs.” The correct answer is “$9.”
This question tests your ability to solve word problems and to interpret a step function graph. A step function is a piecewise, constant function where the constant pieces are observed over different intervals.
- When looking at the two graphs for the taxi cab companies, we see that both are graphs of step functions. The graph looks like discontinuous stairs, and each value consists of a closed circle connected by a horizontal line to an open circle.
- The open circles indicate that the point is not actually on the graph, while the closed circles indicate inclusion of that point on the graph.
- Thus, when interpreting the fares for the two cab companies, we only pay attention to the closed circles, since those are the ones whose values are real.
- For a 5 mile trip with ABC Cabs, the graph shows that the closed circle corresponds to a value of $12 at miles = 5. For a 5 mile trip with Tary Taxicabs, the graph shows that the closed circle corresponds to a value of $9 at miles = 5.
- The cheaper fare for a 5-mile trip is $9 with Tary Taxicabs, since $9 is less than $12.
Question 49, “Area of the region bounded by the graph.” The correct answer is “13.”
This question tests your understanding of geometry.
- The region bounded by the graph of y = f(x), the y-axis, and the x-axis can be split into a trapezoid and a triangle by extending a horizontal line segment from (2,3) to (0,3).
- From here, we can first calculate the area of the trapezoid, which is given by
, where and a and b are the bases of the trapezoid and h is the height.
- We can see that the first base of the trapezoid is 5 units long because it extends from the origin to the point (5,0). The second base of the trapezoid extends from (0,3) to (3,3), so it is 3 units long.
- Meanwhile, the height of the trapezoid is 3 units because the y-coordinate of (3,3) is 3 units away from the origin.
- Plugging these values into the formula for the area of a trapezoid gives us
, which can be simplified into A = 4•3. The area of the trapezoid equals 12 square units.
- Next, we must find the area of the triangle that is enclosed by the points (2,3), (0,3), and (0,4). The area of a triangle is given by
.
- The base of the triangle is 2 units long (this is determined by subtracting the x-coordinate of (0,3) from the x-coordinate of (2,3). The height of the triangle is 1 unit, and this is determined by subtracting the y-coordinate of (0,3) from the y-coordinate of (0,4).
- Plugging these values into the formula for the area of a triangle gives us
, which can be simplified into
square unit.
- The total area of the region bounded by the graph y = f(x), the y-axis, and the x-axis equals 12 square units plus 1 square unit, which gives us a value of 13 square units.
Question 50, “Sum of 2 positive numbers.” The correct answer is “91.”
This question tests your understanding of solving algebraic equations.
- First, set up equations to represent the statements in the question. Let
equal the lesser number and
equal the greater number.
- We are able to set up these equations:
and
. We want to find
- The first step to solving these equations is to plug the equation for x into the equation of the sum of the two numbers. This gives us
.
- Next, subtract 19 from each side to get
. Subtract y from both sides to isolate
. This gives us
.
- Next, square each side to get
, which can be simplified into
.
- Set this equation to zero by subtracting y from each side. This gives us the equation
, which can be solved using the quadratic formula. The quadratic formula is
.
- Plugging in the corresponding values for a, b, and c based on the equation form of
. This gives us
.
- We can further simplify this equation to get
.
- From here, we can either add 23 to 265 or subtract 23 from 265. If we add 23 to 265, we find that
. If
, then
. We can plug these values back into the equation for the value of x to see if they match up.
- Plugging in these values gives us
. 7 is clearly not greater than 19 + 12, so the value of y cannot be 144.
- Now, we can try to subtract 23 from 265, which gives us that
. If
, then
(calculated by subtracting 121 from 151).
- Plugging these values back into the equation for x gives us
. This can be simplified into
. This confirms that
and
.
- The value of the greater number minus the lesser number is simply 121 minus 30, which equals 91, the correct answer.
Question 51, “41, 35, 30, X, Y, 15.” The correct answer is “26.”
This question tests your understanding of averages and values in lists. The average of a list of values is equal to the total sum of these values (numerator) divided by the number of items in the list (denominator). The median of a list is the middle number in a sorted (ordered based on numerical value) sequence. The mode of a list is the number that occurs the most often in a set of numbers.
- We know that the list currently contains the numbers 41, 35, 30, X, Y, and 15. The mode of the list is 15, which means that the number 15 must occur more than once in this list. Therefore, Y must be 15.
- Meanwhile, the median of the list is 25. In a list of even numbers, the median is found by taking the average of the middle two numbers, which are 30 and X in this case.
- We can write this as
. This equation can be simplified by multiplying each side by 2 to get
. Subtracting 30 from each side gives us
.
- Now that we know the value of X and Y, we can find the mean of the list, which is found by dividing the total sum of the list by the number of items in the list.
- This is represented by
, which can be simplified into
. This gives us M = 26, which is the correct answer.
Question 52, “rx+sy = t.” The correct answer is “.”
This question tests your understanding of systems of equations and the quadratic formula, which is denoted as .
- We are given the system of equations:
and
. First, substitute y for x2.
- This gives us
. Next, subtract t from each side so that the equation can be set to 0.
- We now have
. This would typically be solved using the quadratic formula,
.
- Looking at the answer choices, they are in the format of the discriminant in the quadratic formula, which is the “
” expression inside the square root of the quadratic formula.
- In order for there to be more than one solution for the system,
has to be greater than 0. From this knowledge, we can set up the inequality
and plug in the corresponding values for a, b, and c.
- a corresponds to s, b corresponds to r, and c corresponds to t. Plugging these values in gives us the inequality
, which is the correct answer.
Question 53, “Arithmetic sequence.” The correct answer is “248.”
This question tests your understanding of arithmetic sequences, which is a list of numbers where the difference between one term and the next is a constant.
- The general rule for the terms of an arithmetic sequence is
, where a is the first term of the sequence, d is the difference between each term in the sequence, and n is the number of terms in the sequence.
- We are given the 3rd and 4th terms of the sequence. From here, we can determine the difference between each term by subtracting 13 from 18 to get
.
- We can also use these terms to figure out the first term of the sequence. If the difference between each term is 5, then the 2nd term = 13 – 5 = 8. From here, the first term must be 8 – 5, which equals 3.
- Now, we can plug these values,
,
, and
into our equation for an arithmetic sequence. This gives us
, which can be simplified into
.
- Further simplification gives us
, which is the correct answer.
Question 54, “Graph of .” The correct answer is
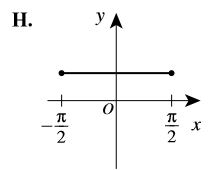 .
.
This question tests your understanding of trigonometry and trigonometric identities.
- The equation for the graph is given as
. This is recognizable as one of the main Pythagorean trigonometric identities:
.
- This means that the graph of
can also be written as
. The graph that correctly depicts this equation is the answer choice with the horizontal line at
.
Question 55, “Period of the function.” The correct answer is “.”
This question tests your understanding of trigonometric functions.
- The normal period of
is
. The function that is given,
, represents a stretching of the
graph vertically along the y-axis by a factor of 4.
- The period of this stretched function is given by
, where b is the coefficient in
. Thus, the period of the function
is
, which equals
.
Question 56, “At the school carnival.” The correct answer is “.”
This question tests your understanding of probability, which is represented as a fraction where the number of possibilities of a certain event occurring (numerator) is divided by the total number of outcomes (denominator).
- The odds of a penny landing heads faceup is
. If it lands heads up, Mike gets 3 points. If not, he gets 0 points. Therefore, the expected value of points awarded for tossing the penny is equal to
, which equals
.
- The expected value of points awarded for tossing a nickel and for tossing a dime are the same. Thus, we can find the expected value of x, Mike’s total number of points, by adding up the individual expected values for each coin.
- We can write this as
, which is the correct answer.
Question 57, “Determinant of the matrix.” The correct answer is “4.”
This question tests your understanding of matrices. A matrix is a rectangular array of numbers, symbols, or expressions that is arranged in rows and columns.
- The question states that the determinant of the matrix
is
. We can apply this to the matrix that we are given.
- For the matrix
,
and
. Applying the determinant definition to this matrix gives us
.
- Thus, the determinant of the matrix can be written as
. We can set this equal to
in order to solve the question.
- This gives us
, which can be simplified by subtracting
from each side. We now have the equation
, which is a quadratic expression that can be factored.
- Both 4 and 3 are factors of 12, and 3 minus 4 is -1, which makes it likely that the two factors are going to be 4 and 3. Thus, we can rewrite
as
- From here, we can solve for k, which gives us
and
. Thus, the determinant of the matrix is equal to k when k equals 4, which is the correct answer.
Question 58, “.” The correct answer is “When n is divided by 4, the remainder is 0.”
This question tests your understanding of imaginary numbers. An imaginary number is a complex number that can be expressed in terms of the square root of a negative number. The general rule for imaginary numbers is that , which means that
.
- The question states that
and that
. We know that
, which means that
.
- The two
terms can be combined due to the addition rule of exponents, which states that
. From this, we get
.
- We know that
. If
, then when n is divided by 4, the remainder is 0. Thus, this is the statement about n that must be true.
Note: There are additional solutions to this equation, as n can be any factor of 4. We know this because is the same as multiplying
by
for an n number of times. Essentially, this is the same as multiplying 1 by 1.
Question 59, “|sinθ|≥ 1.” The correct answer is ““.
This question tests your understanding of trigonometric functions.
- We know that
for all values of θ (because sin cannot extend beyond the unit circle, whose radius is 1). Therefore, since we know that sin cannot be greater than 1, we simply have to focus on where sinθ = ±1.
- We know that sinθ = ±1 when
and
, because these are the radians at which the y-coordinate of the unit circle is equal to 1.
- Thus, the answer is
.
Question 60, “Ray PK.” The correct answer is “66°.”
This question tests your understanding of geometry.
- Note: This question is easiest to deal with if you can draw a visual representation of
with the ray
bisecting it. Since Ray
is bisecting
, we know that
.
- The measure of the overall angle is equal to
, while the measure of
is
.
- First, let us set up an equation so that we can solve for x. Two times
is equal to the measure of
.
- We can write this as
, which can be simplified by distributing the 2 inside the parenthesis. This gives us
, which can be further simplified by subtracting 8x from both sides.
- From here, we have
, and we can solve for
.
- Now that we have solved for x, we can substitute the value of x into the expression for the measure of
, which is equal to the measure of
.
- This gives us
, which simplifies into
. Thus, the measure of
is 66°, which is the correct answer.




Leave A Comment