
As you begin preparing for the math section of the ACT, an important early step is to get a firm grasp on the most essential ACT math topics. Armed with this knowledge, you can face down an entire section based entirely on math and turn it from something intimidating to something empowering!
In this ACT math topics review, we will go over the 12 different ACT math question types; then, we will point you toward some winning ACT math strategies and test preparation resources. Finally, we will discuss the importance of maintaining your mental health as you enter this exciting stage of preparation. Read on to learn all about how Piqosity will be able to help you prepare for the ACT!
What are the Math Topics on the ACT?
By and large, you can expect to encounter ACT math topics that you have already seen before: very few ACT math questions deal with topics you learn in your senior year of high school. Approximately half of the problems on this section cover Algebra and approximately 40% of the problems cover geometry. The remaining 10% covers concepts covered in middle school, and some problems over high school Pre-calculus. You will need to know basic formulas, but don’t stress about more complex formulas. Keep in mind, formulas are not provided during the test, so you will need to have those basic concepts memorized.
Here is a comprehensive ACT math topics list, along with a percentage that indicates how much each section affects your overall score.
Algebra (~50%)
1. Exponent Rules
A strong knowledge of the rules governing exponents is essential for this section.
You may be asked problems that involve simplifying expressions using one or many of the rules below.
A firm foundation of exponent rules also makes solving problems on scientific notation much easier for most students.
2. Factoring 2nd & 3rd order polynomials
You will be asked to factor 2nd and 3rd order polynomials using common algorithms such as factoring using factor trees, using the difference of squares, difference of cubes, factoring by grouping or using the quadratic formula. An essential skill that assists with this section is a knowledge of common squares and cubes.
Example:
Factor the following polynomial.
5x2 + 10y + x2y + 2y2
Solution:
There is no common factor that exists for all terms of this polynomial; y, for instance, is common for three of the terms, but it is not a factor of 5x2.However, this polynomial can still be factored through the grouping method. The grouping method requires common factors to be found for groups of terms within the polynomial.
As shown below, there is a common factor of 5 in the first 2 terms of the polynomial, and there is a common factor of y in the last two terms of the polynomial. These terms are factored out:
5(x2 + 2y) + y(x2 + 2y)
Now, notice that our factored form does have a GCF: x2 + 2y. So, we can now factor out the GCF to get:
(5 + y)(x2 + 2y)
If these two polynomials were to multiplied, the original polynomial (5x2 + 10y + x2y + 2y2) would be the resulting answer.
3. Writing & solving systems of equations using substitution and elimination
Understand how to write systems of equations from word problems, then apply either the substitution or elimination method to solve a problem.
Example:
Solve the following system of equations using elimination:
y + 2x = 5
3y − x = 8
Solution:
First, we will check to see if any of the variables can be eliminated by adding the two equations together. This is not the case, so we need to manipulate one of the equations to be able to eliminate one of the variables. This can be done by multiplying the first equation by 3 to cancel out the y variable or by multiplying the second equation by 2 to cancel out the x variable. Notice that if we multiply the second equation by 2, we will be able to directly cancel out 2x with −2x, so this is likely the easiest option:y + 2x = 5
6y − 2x = 16Now, we can add the two equations together and solve for y.
7y = 21
y = 3
We can plug this value back into either equation to solve for x.
y + 2x =5
3 + 2x = 5
2x = 2
x = 1
The solution to this system is (1, 3).
4. Statistics and Probability
Questions in this category will require you to analyze different methods of data collection, calculate probabilities, and more.
Example:
What is the probability of flipping a coin and landing on heads three times in a row?
Solution:
The probability of flipping a coin and landing on heads is:
Since we are trying to solve for the probability of getting heads 3 times in a row, we will need to multiply the probability of getting heads by itself 3 times.
This means that there is a 1 in 8 probability of getting heads 3 times in a row when flipping a coin.
5. Linear Equations
These questions test your understanding of how to model straight lines.
Geometry (~40%)
1. Triangles
Understand the different properties for the 4 main types of triangles: equilateral, isosceles, right triangle, scalene.
Compute the perimeter and area of a triangle.
2. Quadrilaterals
Find the perimeter and area for different quadrilaterals such as squares, rectangles, parallelograms, kites and trapezoids.
3. Circles
Find the circumference and area of circles, or slices of circles.
4. Pythagorean Theorem
Understand when to apply the Pythagorean theorem to solve problems involving triangles.
5. Coordinate Geometry
Know how to read a graph and how to find the distance and midpoint between two points on a coordinate plane.
Pre-Calculus (~5%)
1. Trigonometry
Know how to convert between radians and degrees, as well as how to evaluate the trig. functions sin, cos and tan to specific angle measures.
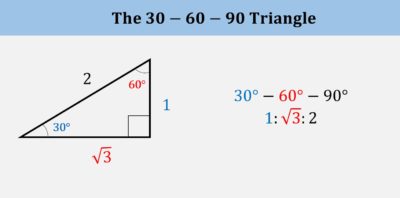
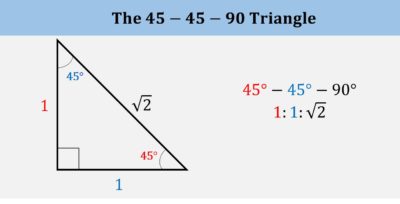
2. Special right triangles
Understand the properties of the 30-60-90 and 45-45-90 special right triangles.
Essential Skills (~5%)
These questions will cover the math skills students should have learned before high school.
- Order of operations
- Constant proportions
- Converting between fractions, decimals and percentages
- Simple and weighted average
Although the skills themselves are fairly straightforward, you may be asked to use them in particularly complex ways. Some atypical problems may require students to combine skills across multiple mathematical disciplines.
Modeling
Modeling is measured throughout all the above categories, but not as its own individual concept. Rather, your score will be determined from your answers above. Broadly speaking, modeling questions are those which ask students to use mathematical skills and concepts to explain or solve real-life problems. Frequently, modeling questions use images, figures, or diagrams.
Looking at the ACT Math Section
Wondering how ACT math questions are formatted? Most ACT math questions are self-contained, but some build off of each other into a set of questions. The best way to build familiarity with these kinds of questions is to practice them! Work through the following examples, and you’ll soon be comfortable with anything the ACT math section has to offer:
- 2021-2022 ACT Official Test Full Answer Explanations
- 2020 ACT Official Test Full Answer Explanations
- 2015-2018 ACT Official Test Full Answer Explanations
Additionally, you’ll likely benefit from a review of our collection of tried-and-true ACT Math Strategies.
This is Your Brain on (ACT) Math
In addition to encouraging you to spend the time to master all of the ACT math question types (and topics), there are two other points we’d like to cover when it comes to your brain and ACT math.
First, remember that this is a timed test. You may want to hone skills with our useful mental math strategies to maximize your limited time. Keep in mind that calculators are allowed during the ACT math test. Having a calculator on hand to assist you can also help with both your time and your score.
Second, we know that math can be a tough subject for many students. If math is not your strong suit, you may be dealing with a significant amount of standardized test anxiety already. Check out these strategies for overcoming math anxiety, and remember to gently prepare over time in the months prior to your ACT test date rather than waiting until the last minute to cram!
Related: Do you suffer from an “I suck at math” mentality? You can change that!
ACT Math Practice with Piqosity!
You don’t need to stress about ACT math topics. You have already encountered them in your regular schooling, and you have months to prepare.
About that preparation: why not use Piqosity’s suite of online ACT test prep? Whether you’re in the process of preparing for your first ACT or you’ve already received your score report and want to know how to improve your ACT Score, Piqosity has you covered.
Joining Piqosity is FREE (no credit card information required, no sneaky fine-print trials). Start off with our mini diagnostic test to get a baseline score, and set realistic goals for your ACT success.
Then, figure out a plan for exactly how you’d like to study. You can continue to use many of Piqosity’s unique features and valuable resources as part of our FREE Community package. But, if you’re ready for the next step, you can choose among several competitively-priced test prep packages, you will have access to up to 10 complete ACT practice tests with answers and explanations.
With Piqosity on your side, you’re ready to start conquering ACT math preparation today!
More Educational Resources by Piqosity:



Leave A Comment